
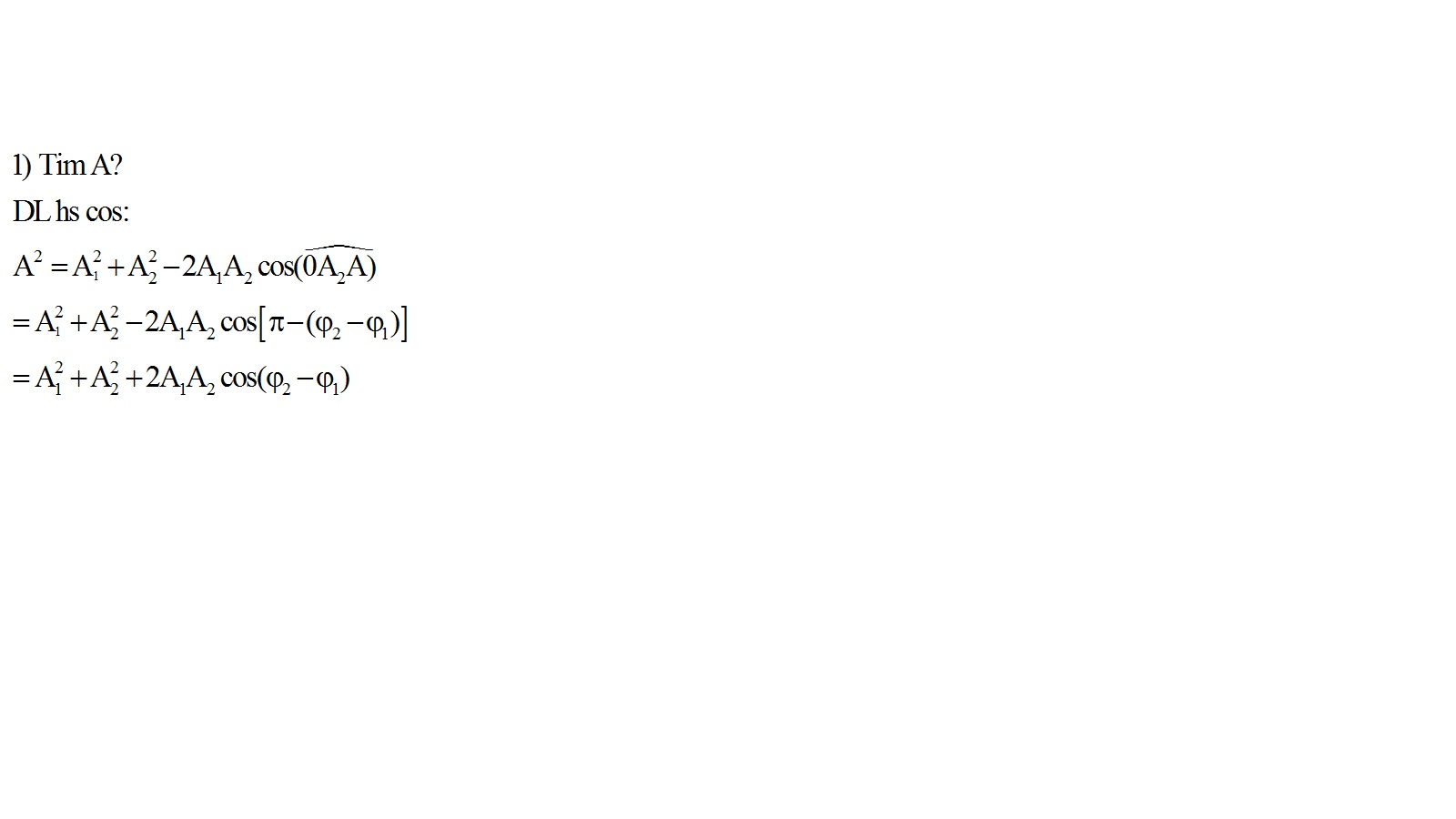
Như vậy biên độ tổng hợp phụ thuộc vào biên độ thành phần và phụ thuộc vào
∆φ = φ2 –φ1
Nếu cả A1, A2 không đổi thì
- A ( max) khi và chỉ khi ∆φ=0
2 dao động cùng pha
Khi đó A1 ↑↑ A2
A ( max) = A1 + A2
- A ( min) khi và chỉ khi ∆φ=±π
2 dao động ngược pha A1 ↑↓ A2
A ( min)= ∥( A1-A2)
Tóm lại:
A ( min) ≤ A ≤ A ( max)
∥( A1-A2) A1+A2

- Nếu pt là 2 dao động thành phần là sin thì phương trình tổng hợp là hàm sin
- Nếu pt dao động tổng hợp là hàm cos , sin thi đổi thành sin sin , cos cos
-Nếu ∆φ> 0 => φ2>φ1
dd 2 sớm pha ( nhanh ) hơn dd 1
- Nếu ∆φ<0 => φ2<φ1
dd 2 trễ pha ( chậm ) hơn dd 1
- Nếu ∆φ=k2π => chẵn lần π
Thì 2 dao động cùng pha 0, ±2π, ±4π
- Nếu ∆φ=(2k+1)π => lẻ lần π
Thì 2 dao động ngược pha ±π, ±3π
- Nếu 2 dao động ⊥ pha
∆φ=±π/2
+ 2 dao động cùng pha ∆φ=k2π
A= A1+ A2
φ= φ1 =φ2
+ 2 dao động ngược pha:
∆φ=(2k+1)π thì A=/A1-A2/
φ= φ1 nếu A1 > A2
φ=φ2 nếu A1 < A2
+ Nếu 2 dao động ⊥ pha:
∆φ=±π/2 => A√(a1)^2+(a2)^2
Tính φ theo công thức
+ Nếu 2 dao động cùng biên độ:
φ=(φ1+φ2)/2